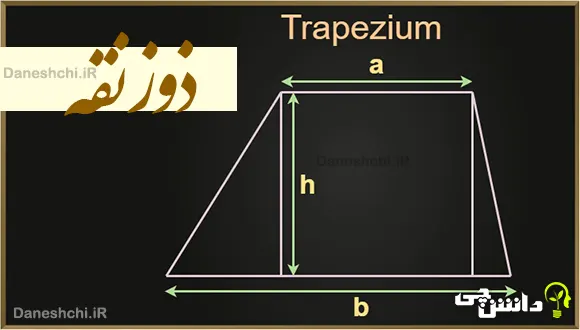
ذوزنقه یک شکل چهارضلعی است که تنها دو ضلع آن با هم موازی هستند. این دو ضلع موازی، معمولاً “قاعده” نامیده میشوند. دو ضلع دیگر آن که موازی نیستند، “ساق” نام دارند.
انواع مختلفی از ذوزنقه وجود دارد:
* **ذوزنقه متساویالساقین:** در این نوع، دو ساق با هم برابرند و زوایای هر قاعده نیز با هم مساوی هستند.
* **ذوزنقه قائمالزاویه:** این ذوزنقه دو زاویه قائمه (۹۰ درجه) دارد.
محیط ذوزنقه مانند همه شکلها، از جمع کردن طول تمام ضلعهایش به دست میآید.
برای محاسبه مساحت ذوزنقه، از این فرمول استفاده میکنیم:
مجموع دو قاعده را با هم جمع میکنیم، سپس حاصل را در ارتفاع ضرب کرده و در آخر بر دو تقسیم میکنیم.
(قاعده بزرگ + قاعده کوچک) × ارتفاع ÷ ۲ = مساحت ذوزنقه
ارتفاع ذوزنقه، فاصله عمودی بین دو قاعده موازی آن است.
در هندسه، تعریفهای گوناگونی از ذوزنقه ارائه شده است. بعضی از افراد آن را یک چهارضلعی با دو ضلع موازی میدانند و برخی دیگر آن را در دستهی متوازیالاضلاعها قرار نمیدهند. پروکلوس، ریاضیدان و فیلسوف یونانی، که روشهای متفاوتی از فیثاغورث در حل مسائل هندسی داشت، چهارضلعیها را به دو گروه متوازیالاضلاع و غیر متوازیالاضلاع تقسیم کرده است. در این نوشته، با بررسی ویژگیها و گونههای مختلف ذوزنقه، بیشتر با این شکل هندسیِ خاص و جالب آشنا خواهیم شد.
تعریف ذوزنقه
کلمه ذوزنقه از دو بخش تشکیل شده است. بخش اول “ذو” به معنای دارا بودن و بخش دوم “زنق” به معنی چانه است. چون این شکل شبیه به چانه به نظر میرسد، به آن ذوزنقه میگویند که یعنی شکلی که چانه دارد.
در هندسه، ذوزنقه یک شکل چهارضلعی بسته است که چهار گوشه دارد. در این شکل، دو ضلع آن با هم موازی هستند و دو ضلع دیگر موازی نیستند و در مقابل هم قرار گرفتهاند.
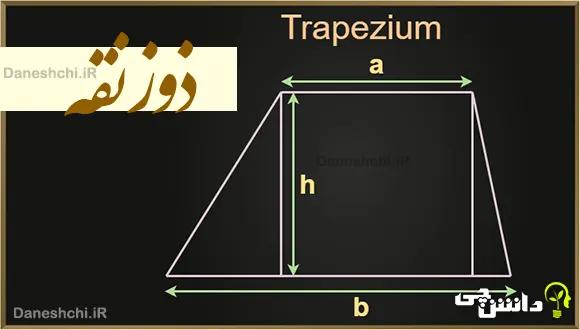
به شکل ذوزنقه در پایین نگاه کنید. اضلاع این شکل AB، BC، CD و AD هستند. در اینجا AB با CD موازی است و به آنها قاعدههای ذوزنقه میگوییم. اما AD و BC با هم موازی نیستند و به آنها ساقهای ذوزنقه گفته میشود. h نیز نشاندهنده بلندی یا ارتفاع ذوزنقه است. شما میتوانید برای اندازهگیری ارتفاع از هر حرفی که دوست دارید استفاده کنید؛ مثلاً به جای h از حرف “ب” برای نشاندادن بلندی شکل کمک بگیرید.
ویژگی های یک ذوزنقه
هر شکل چهارضلعی ویژگیهای مخصوص به خودش را دارد که باعث میشود بتوان آن را از بقیه اشکال تشخیص داد. این خصوصیات، در واقع ساختار هندسی آن شکل را میسازند.
ذوزنقه یک شکل هندسیِ دو بعدی است.
در ذوزنقه، دو ضلع که به آنها پایه میگوییم با هم موازی هستند.
دو زاویهای که در کنار هر ضلع غیرموازی قرار گرفتهاند، اگر با هم جمع شوند، حاصل ۱۸۰ درجه خواهد بود.
ذوزنقه دو ضلع موازی و دو ضلع غیر موازی دارد.
اگر همه زوایای داخل ذوزنقه را با هم جمع کنیم، همیشه به عدد ۳۶۰ درجه میرسیم.
ذوزنقه دو خط دارد که رأسهای مقابل را به هم وصل میکنند که به آنها قطر میگوییم. برخلاف بعضی از چهارضلعیهای دیگر، این دو قطر با هم برابر نیستند. طول قطرهای ذوزنقه به اندازهی پایهها و زوایای آن بستگی دارد. این دو قطر همیشه یکدیگر را قطع میکنند.
انواع ذوزنقه
ذوزنقهها بر اساس ویژگیهای اضلاع و زوایایشان به سه گروه اصلی تقسیم میشوند.
ذوزنقه مختلف الاضلاع
ذوزنقهای که هر چهار ضلع آن طول متفاوتی دارند و هیچ دو ضلعی با هم مساوی نیستند، یک ذوزنقه مختلفالاضلاع نامیده میشود. در این نوع ذوزنقه، اندازهی زاویهها نیز با هم متفاوت است. برای اینکه راحتتر آن را به خاطر بسپارید، میتوانید از عبارت “ذوزنقه نامنظم” برایش استفاده کنید.
ذوزنقه متساوی الساقین
ذوزنقهای که دو ساق آن دقیقاً هماندازه و برابر باشند، ذوزنقه متساویالساقین نام دارد. در این نوع ذوزنقه، دو ضلع که با هم موازی نیستند، طول یکسانی دارند. به همین دلیل میتوان آن را نوعی ذوزنقه منظم در نظر گرفت.
ذوزنقه قائم الزاویه
ذوزنقهای که یکی از ساقهای آن با هر دو پایه زاویه قائمه (۹۰ درجه) بسازد، ذوزنقه قائمالزاویه نامیده میشود. این نوع ذوزنقه نیز مانند ذوزنقه معمولی، دارای اضلاعی با اندازههای مختلف است. تفاوت اصلی در این است که در ذوزنقه قائمالزاویه، دو زاویه راست (۹۰ درجه) وجود دارد.
فرمولهای مهم ذوزنقه
فرمولهای اصلی و کاربردی برای محاسبهی ویژگیهای یک ذوزنقه به شرح زیر است:
**محیط ذوزنقه:**
برای به دست آوردن محیط، کافی است طول هر چهار ضلع را با هم جمع کنید.
`محیط = قاعده بزرگ + قاعده کوچک + ساق چپ + ساق راست`
**مساحت ذوزنقه:**
مساحت از طریق این فرمول محاسبه میشود:
`مساحت = ( (قاعده بزرگ + قاعده کوچک) × ارتفاع ) ÷ ۲`
به بیان دیگر، میانگین دو قاعده را در ارتفاع ضرب کنید.
مساحت
برای محاسبه مساحت یک ذوزنقه، ابتدا باید میانگین دو قاعده آن را به دست آوریم. این کار را با جمع کردن اندازه دو قاعده و تقسیم نتیجه بر دو انجام میدهیم. سپس حاصل این میانگین را در ارتفاع ذوزنقه ضرب میکنیم. بنابراین، مساحت برابر است با: نصف مجموع دو قاعده ضربدر ارتفاع.
محیط
برای محاسبه دور یک شکل ذوزنقهای، کافی است اندازه هر چهار ضلع آن را با هم جمع کنید. بنابراین، محیط این شکل برابر خواهد بود با مجموع اندازههای AB و BC و CD و AD.
میانه مرکزی
خط میانه در یک ذوزنقه، پارهخطی است که وسط دو ساق آن را به هم وصل میکند. این خط با هر دو قاعده ذوزنقه موازی است و طول آن دقیقاً برابر است با میانگین طول دو قاعده. یعنی اگر طول قاعدهها را AB و CD در نظر بگیریم، طول خط میانه از فرمول زیر به دست میآید:
(AB + CD) ÷ ۲
رابطه ذوزنقه و متوازی الاضلاع
در شکل ذوزنقه، تنها دو ضلع با هم موازی هستند. اما در متوازیالاضلاع، هر دو ضلع روبرو با هم موازی میباشند.
همچنین در متوازیالاضلاع، اضلاع روبهرویی همطول هستند، در حالی که در ذوزنقه این دو ضلع لزوماً برابر نیستند.
متوازیالاضلاع شامل شکلهایی مانند مستطیل، مربع و لوزی میشود، اما ذوزنقه به دلیل تفاوت در اندازه اضلاعش، خارج از این دسته قرار میگیرد.
بنابراین میتوان گفت ذوزنقه نوعی متوازیالاضلاع است که فقط دو ضلع آن موازی هستند.